Поведение потребителя

Сглаженный ряд уровней по трехлетним короче фактического на 1 член ряда в начале и в конце ряда, по 5 летним - 2 члена в начале и в конце ряда. Он меньше, чем фактический подвержен колебаниям из-за случайных причин и в виде некоторой плавной линии выражает основную тенденцию роста урожайности за изучаемый период, связанный с действием долговременно существующих причин и условий развития.

Недостатком оглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, потеря информации.

Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.

. Метод аналитического выравнивания

Для того, чтобы дать количественную модель выражающую основную тенденцию изменения уровня динамического ряда во времени используется аналитическое выравнивание ряда динамики. Основное содержание метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается, как функция времени:

где -уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Выбор типа модели зависит от цели исследования и должно быть основано на теоретическом анализе, выявляющем характерность развития явления, а также на графическом изображении ряда динамики.

В тех случаях, когда требуется особо точное изучение тенденции развития при выборе вида адекватной функции можно использовать специальные критерии математической статистики.

Расчет параметров функции обычно производиться методом наименьших квадратов в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпирическими уравнениями.

Параметры уравнения ai удовлетворяющие этому условию могут быть найдены решением системы нормальных уравнений. Рассмотрим технику выравнивания ряда динамики по прямой

.

Параметры a0,a1 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:

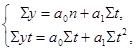
у - фактические (эмпирические) уровни ряда;

t - время или порядковый номер периода или момента времени;

Расчет параметров значительно упрощается, если за начало отсчета времени (Σt = 0), принять центральный интервал или момент.

При четном числе уравнений (например 6) значение t условного обозначения времени будут такими:

Таблица 4

Условные обозначения времени

2002 г.	2003 г.	2004 г.	2005 г.	2006 г.	2007 г.
-5	-3	-1	+1	+3	+5

При нечетном числе уравнений (например 7), значения устанавливаются по другому:

Таблица 5

Условные обозначения времени

2001	2002	2003	2004	2005	2006	2007
-3	-2	-1	0	+1	+2	+3

В обоих случаях ∑t = 0, тогда система нормальных уравнений примет вид:

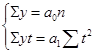
Из первого уравнения

Из второго уравнения Перейти на страницу: 1 2 3 4 5 6 7

Читайте также: