Поведение потребителя

Средняя арифметическая для интервального ряда

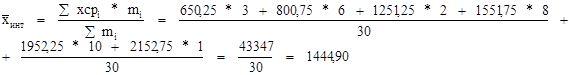
где хсрi - центр i-ого интервала;

mi - частота в i-ом интервале

Мода и медиана

1) для дискретного ряда

При четном числе вариантов медиана будет равна средней арифметической из двух срединных вариантов.

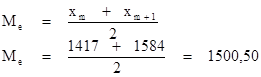
2) для интервального ряда

Медианным является первый интервал, для которого ∑mi превышает половину от общего числа наблюдений. Т.е. интервал 1401,5 - 1702 - медианный.

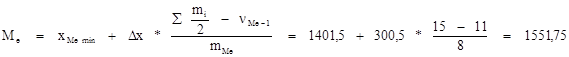
где хМеmin - нижняя граница медианного интервала;

∆х - длина интервала;

- половина накопленных частот;

νm-1 - накопленная частота интервалов, предшествующая медианному интервалу

mMe - частота медианного интервала.

Мода -

это вариант, наиболее часто встречающийся в данном вариационном ряду.

1) для дискретного ряда - это вариант с наибольшей частотой.

Мо1 = 1417;

2) для интервального ряда определяют модальный интервал по наибольшей частоте (mМо = 10)

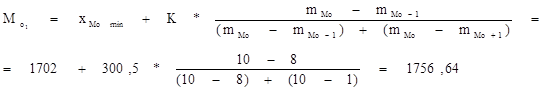
где хМоmin - нижняя граница модального интервала;

К - величина интервала;

mМо - частота интервала;

mMo-1 - частота интервала, предшествующего модальному;

mMo+1 - частота интервала, следующего за модальным.

Показатели вариации

1. Размах вариации:

R = xmax - xmin = 2300-500=1800

. Среднее линейное отклонение (для интервального ряда):

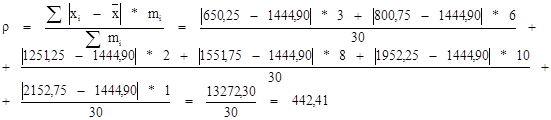
3. Дисперсия:

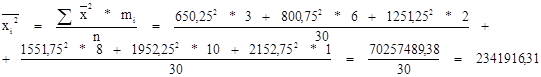
где - средняя из квадратов значений признака;

- квадрат средней арифметической;

4. Среднее квадратичное отклонение

5. Коэффициенты вариации:

Перейти на страницу: 1 2 3 

Читайте также: